一个二阶马尔可夫信源，符号集A= {0,1}，符号转移概率为：p（0|00)=0.75，p（0|10)=0.5，p（0|01)=0.8，p（0|11)= 0.6。（1)写出信源的状态转移概率矩阵。（2)求信源的平稳状态分布。（3)计算信源的极限熵。（4)求信源单符号平稳概率分布p（x1)。（5)求平稳一阶转移概率p（x2|x1)。（6)求一阶条件熵H（X2|X1)。

有一个二元二阶马尔可夫信源，其信源符号集为{0，1}，初始概率大小为

P(0)=1/3，P(1)=2/3。 条件转移概率P(0|00)=P(1|11)=0.8，

P(1|00)=P(0|11)=0.2, P(0|01)=P(0|10)=P(1|01)=P(1|10)=0.5

设m阶马尔可夫信源S，其符号集A={x₁，x₂，…x_q}，又设p₁，p₂，…，p_q为其平稳后的一维概率分布，现定义一无记忆信源，它的符号集也是A={x₁，x₂，…，x_q}，又其符号概率分布等于m阶马尔可夫信源S平稳后的一维概率分布，称信源为m阶马尔可夫信源的伴随信源，试证明。

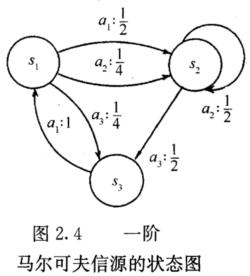
求出图中马尔可夫信源的状态极限概率并找出符号的极限概率。

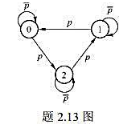
一阶马尔可夫信源的状态图如题2.13图所示。信源X的符号集为{0, 1,2}。

(1)求平稳后信源的概率分布:

(2)求信源的熵H∞。

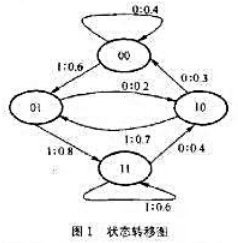
一个二元二阶马氏源， 符号集{0,1}，状态转移图如图1所示。

(1)写出此马氏源的状态转移概率矩阵。

(2)求此信源的平稳状态分布和对应的单符号概率分布。

(3)求此马氏源的符号熵。

(4)求H₀、H₁、H₂、H₃和信源的冗余度。

设包含3个符号的等概率信源X，试验信道输出符号集含2个符号，失真矩阵为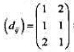：求D_min，D_max与对应的试验信道转移概率。

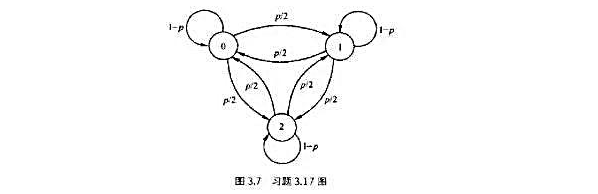
一个一阶马氏源的状态转移图如图3.7所示，信源符号集为(0，1，2);求:

(1)信源的平稳分布;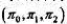

(2)信源的符号熵:

(3)当p为何值时，信源的符号熵达到最大值？当p=0或1时，结果如何？

(4)如果将信源看成无记忆的且以平稳分布为概率分布，求信源的熵。

设马尔可夫链的转移概率矩阵为

求每一个不可约闭集的平稳分布．